Biofluids and Biotransport
Laboratory
Location: RRB 107B
Investigators: Drs
S.S. Sadhal & Anita N. Penkova
Ocular Drug
Delivery
Retinal Diseases and Transport Processes: Retinal diseases affect the
neurosensory tissue in the posterior segment of the eye. Two of the most
prevalent retinal diseases include macular edema from diabetic retinopathy and
neovascular age-related macular degeneration, are significant causes of visual
impairment worldwide, especially among the elderly population. Approximately 15 million
people in the United States have AMD, and more than 1.7 million Americans
suffer from advance stages of this disease.
This
number is expected to grow to nearly
3 million by 2020. With the ocular system, as for most other
physiological systems, fluid transport is a common parameter participating in
maintaining health and nutrition as well as an active drug transporter for
disease-related intervention. Delivering drugs to the posterior segment of
the eye requires detailed information about the transport mechanisms and major
diffusion barriers present in the eye. While advances have been made in the area of drug delivery, several open questions
relating to the feasibility, maintenance of drug levels within a desired
optimum concentration range and achievement of more effective therapies still
remain. Mathematical and computational models and
analysis on mass transport mechanisms of the drug have proven to be effective
tools for better understanding and predicting the transport process in the
posterior part of the eye.
Challenges
While topical eye-drop
administration is considered among the least invasive, its effectiveness for
retinal absorption is limited accompanying side-effects arising from systemic
absorption are high. Intravitreal and transscleral administration have
therefore gained favor. Systemic therapy and topical eye drop administration
deliver low drug levels to the retina and the potential for systemic drug
absorption and the accompanying side effects are high. Due to the effectiveness
of intravitreal delivery methods in delivering the required dose levels ranges
without the expense of systemic exposure, we have focused on this treatment
method for vitreoretinal diseases. In
addition to the side effects, there are several limitations of many of the drugs used for the treatment of vitreoretinal diseases. While the development of these drugs indeed required the expertise of
biochemists and pharmacologists, the delivery mechanisms to focused targets
demands understanding and knowledge of transport phenomena, together with the
fluid mechanics. In order to control the drug delivery
rate for achieving maximum effectiveness, it is vital that we develop the
capability to predict the drug concentration distribution. The predictive model
needs to take into consideration the various transport mechanisms such as
diffusion and convection, as well as saccadic motion. One of the important
outcomes from successful predictive models (accompanied by sound experiments)
will be the drug distribution to the entire vitreous, including the
delivery rate to the back of the eye, particularly the retina, in terms of the
input parameters.
There are numerous challenges concerning drug delivery to the posterior of the eye resulting from the various physiological and anatomical transport barriers that affect the concentration distribution of the drug. Optimal levels of localized drug concentration are highly desirable since low concentrations are often insufficient for the treatment of retinal disease, and with high concentrations toxicity can be an issue. Therefore, the minimization of unnecessary drug concentration in healthy tissues is imperative. Although delivery via the vitreous provides the mechanism for high concentrations in the retina, the relevant surgical procedure (injection or implant) carries with it the risks of side effects such as cataract, retinal detachment, and endophthalmitis. However, the use of intravitreal corticosteroids for DME and intravitreal injections of anti-vascular endothelial growth factor (VEGF) for CNV have revolutionized the treatment of these diseases.
Mathematical
Modeling of Fluid Transport and Ocular Drug Delivery (NEI/NIH Grant No.:
1R01EY026599 - 01A1)
Under the current project, extensive experimental and analytical work is underway on the development of a comprehensive eye model for fluid mechanics and transport phenomena. For such a model, while the differential equations describing the transport processes can be implemented, the biophysical properties for ocular tissue require accurate measurement. We have embarked upon this task, and in the present phase of this work, the following tasks are underway:
1.
Hydraulic
Conductivity Measurement of the Vitreous Humor and the Hyaloid Membrane.
The hydraulic conductivity of the vitreous
humor and the hyaloid membrane have been measured for the bovine eye. In a forthcoming publication, we have taken
on the novel approach of measuring the combined hydraulic conductivity of the
vitreous with the hyaloid intact, as well as with the vitreous broken. This
method, applied to fresh bovine eyes (Manning Beef, Pico Rivera, CA), has
allowed us to obtain the permeability of the hyaloid membrane which is
otherwise extremely difficult to isolate and carry out measurements on. For the
hydraulic conductivity measurement of the vitreous alone, we proposed and
applied the drainage technique whereby the vitreous, placed in an upright
cylindrical chamber, was allowed to drain its liquid
content. Hydrostatic back-pressure 
was applied at the exit by a vertical tube running
about 80cm below the exit of the chamber. The height 
of the vitreous body was recorded as a function of time,
and theoretical model for this history was developed. Specifically, we obtained
following new result,
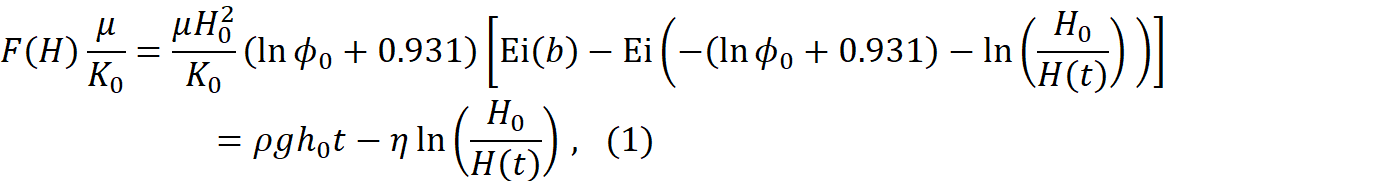
where 
represents the hyaluronic acid and collagen
volume fraction in the vitreous at start, 
is the initial height, 
is the viscosity of the liquid phase is the
vitreous, 
is the gel viscosity, and 
is the hydraulic conductivity of the fully
hydrated vitreous. The least-squares best fit (see Figure 1) for the
experimental values of with this equation, with 
floating, gave the value of 
m2/s.
The novel features here include the implementation of rigorously-established
variation of the Darcy parameter 
with diminishing liquid volume and thus
increasing hyaluronic acid, and collagen volume fraction 
.
For the hydraulic resistance of the vitreous with the hyaloid membrane
intact, the carefully-extracted whole bovine vitreous was placed in the
cylindrical chamber (the cell) with the flat ends supported by 20
nylon
filters with 14% open area. Hydrostatically pressurized saline (20-120 cm head)
was fed in at one end and allowed to percolate through the cylindrically-shaped
vitreous body. The exiting saline was collected over recorded periods and the
flowrates were measured and implemented into the Darcy’s equation to yield the
effective hydraulic conductivity of the intact vitreous. The data are being
collected to be analyzed.
2.
Diffusion
Coefficient of the Vitreous Humor
As a part of the overall goal of the development of a comprehensive
mathematical model for ocular fluid dynamics and drug delivery, we are
measuring the diffusion coefficient of the vitreous humor to various surrogate
drugs. The accuracy afforded by MRI visualization has been demonstrated to be
quite remarkable (see Penkova et al., Int. J. Heat Mass Transfer 70, 504-514, 2014). Since the
development of the technique, we have instituted substantial improvements for
application to Gd-Albumin (galbumin)
and Immunoglobulin (IgG), besides on Gd-DTPA (Magnavist) and Prohance. Galbumin and IgG are available as MRI contrast agents (Biopal, Inc.), and have molecular weights 74, and 149 kDa, respectively, as representative sizes of
macromolecules. The measurement technique entails injection of the contrast
agent into the middle vitreous of an ex vivo bovine eye and tracking the
diffusion of the agent. The imaging data provides information to construct
concentration contours around the injected region, and quantitative comparison
and least-squares best fit of these with theoretically predicted contours
provides the value of the diffusion coefficient. The main new feature is the
implementation of a finite-element code to better fit irregularly-shaped
boluses, as is the case for many of the larger molecules. The theoretical and
the experimental diffusion-front contours are exhibited in Figure 2.
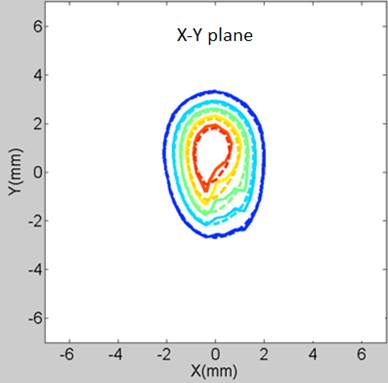
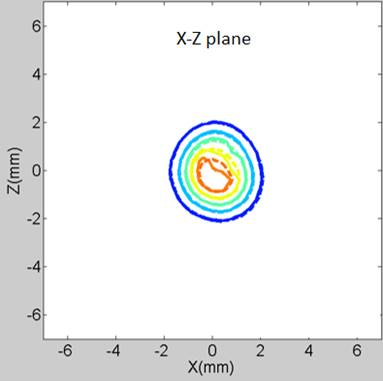
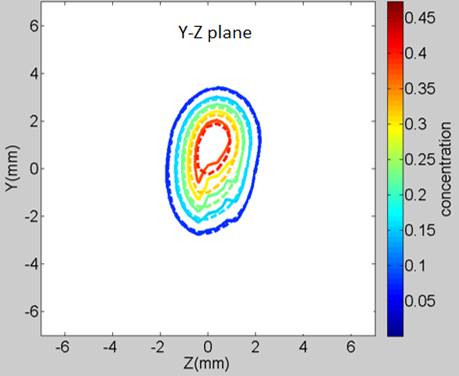
Figure 2: An example of the theoretical and experimental concentration-front contours. The drug surrogate is Immunoglobulin-Gd (IgG, 149 kDa) at 169 min after injection (─── : measurement, ---- : finite element analysis)
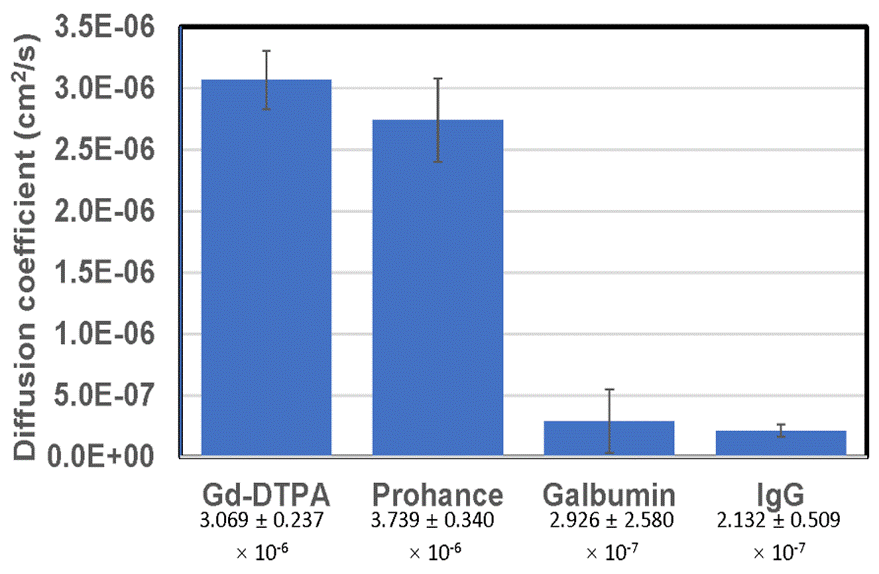
Figure 3: A comparative chart of the Diffusion coefficient values measured by MRI for (1) Gd-DTPA ); (2) Prohance; (3) Galbumin; (4) Immunoglobulin-Gd.
A comparison of the diffusion-coefficient values is given in Figure 3
where we see that the large molecules (Galbumin and
IgG) have a factor of 10 lower diffusion coefficient compared with Gd-DTPA and Prohance. This goal
has been met to the extent defined in the timeline. See draft manuscript of the
publication in preparation http://ruk.usc.edu/bio/sadhal/Biotransport/DiffusionCoeff-2017.pdf
3.
Permeability
Measurements
See details at:
http://ruk.usc.edu/bio/sadhal/Biotransport/MembranePermeability-2017.htm
4.
Hindrance
Coefficient
The proper implementation of convective transport in gel portion of the
vitreous requires the introduction of a resistive parameter (known as the Staverman filtration coefficient). We shall refer to it as
the hindrance coefficient. This is necessary since without it the theory
assumes the convective transport of the large molecule solute to be at the same
rate as the solvent, aside from diffusion, and can overestimate the transport
rate depending on the sizes of macromolecules. We have demonstrated in earlier
studies that with very high water flow rates in ex vivo bovine eyes, while the water
pushes the surrogate, significant residue of the latter remains. For more details see
5.
Simulation of drug transport in the
eye
Finite-difference modeling
for the non-syneretic eye has been initiated with
full implementation of the boundary conditions in the vitreous region using Matlab. At the same time, a preliminary code based on
estimated flow conditions has been developed using STAR-CCM+. Both models are
based on Darcy flow in the vitreous, with water source at the hyaloid region
and the RPE-choroid as the sink. The STAR-CCM+ is a packaged solver and offers
less flexibility for the rigor, numerical accuracy and control. The in-house
code development with Matlab affords greater
flexibility in this regard and will be the one eventually in place for this
project. With the developments based on STAR-CCM+, we have been able to provide
animation of the drug-delivery process. More details and animations of
numerical work are available at
http://ruk.usc.edu/bio/sadhal/Biotransport/NumericalSimulations.htm
The water flowrate is set artificially set much higher than the physiological rate in order to obtain a quick visual of the drug transport process. For the animation setup, this has the same effect as speeding the clock.